Are You Sure This Embedding Is Good Enough?
Suppose you are given a data set of five images to train on, and then have to classify new images with your trained model. Five training samples are in general not sufficient to train a state-of-the-art image classification model, thus this problem is hard and earned it’s own name: few-shot image classification. A lot has been written on few-shot image classification and complex approaches have been suggested.1 Tian et al. (2020), however, suggest it suffices to take an embedding from a different image classification task, extract features from the five images via the embedding, and to train the few-shot model on the embedded version of the five images. For prediction, the new image can be embedded as well and then predicted via the trained model. This alone beats all previous approaches:
In this work, we show that a simple baseline: learning a supervised or self- supervised representation on the meta-training set, followed by training a linear classifier on top of this representation, outperforms state-of-the-art few-shot learning methods.
The premise of “Rethinking Few-Shot Image Classification: a Good Embedding Is All You Need?” by Tian et al. (2020) sounds too good to be true: They essentially follow the steps you might know from fine-tuning of or transfer learning with a pre-trained image classifier—with the only difference that they use five images to fit a new head for their model.
A Naive Example with (Fashion-)MNIST and UMAP
To reason in more detail about the paper’s premise, let’s look at a simple example: Suppose we have five images from the Fashion-MNIST data set; are we able to predict a new image from the same data set if all we have are those five images and a pre-trained embedding? As embedding, we’ll use a simple UMAP trained on a “similar” data set: MNIST.
Since Fashion-MNIST was designed as drop-in replacement for MNIST, we are dealing in both cases with 28x28 grey-scale pixels. At the same time, it isn’t obvious that the embedding trained on MNIST is a useful feature extraction device for Fashion-MNIST.
So the steps are as follows:
- Train UMAP embedding on MNIST train data set2
- Project the Fashion MNIST train and test data onto the trained embedding
- Take five random samples from the Fashion MNIST train data and predict a sample from the Fashion MNIST test data using the nearest neighbor3
As usual with UMAP, we get a useful embedding of the MNIST data set. Here, we show the MNIST test set that has been projected onto this embedding:
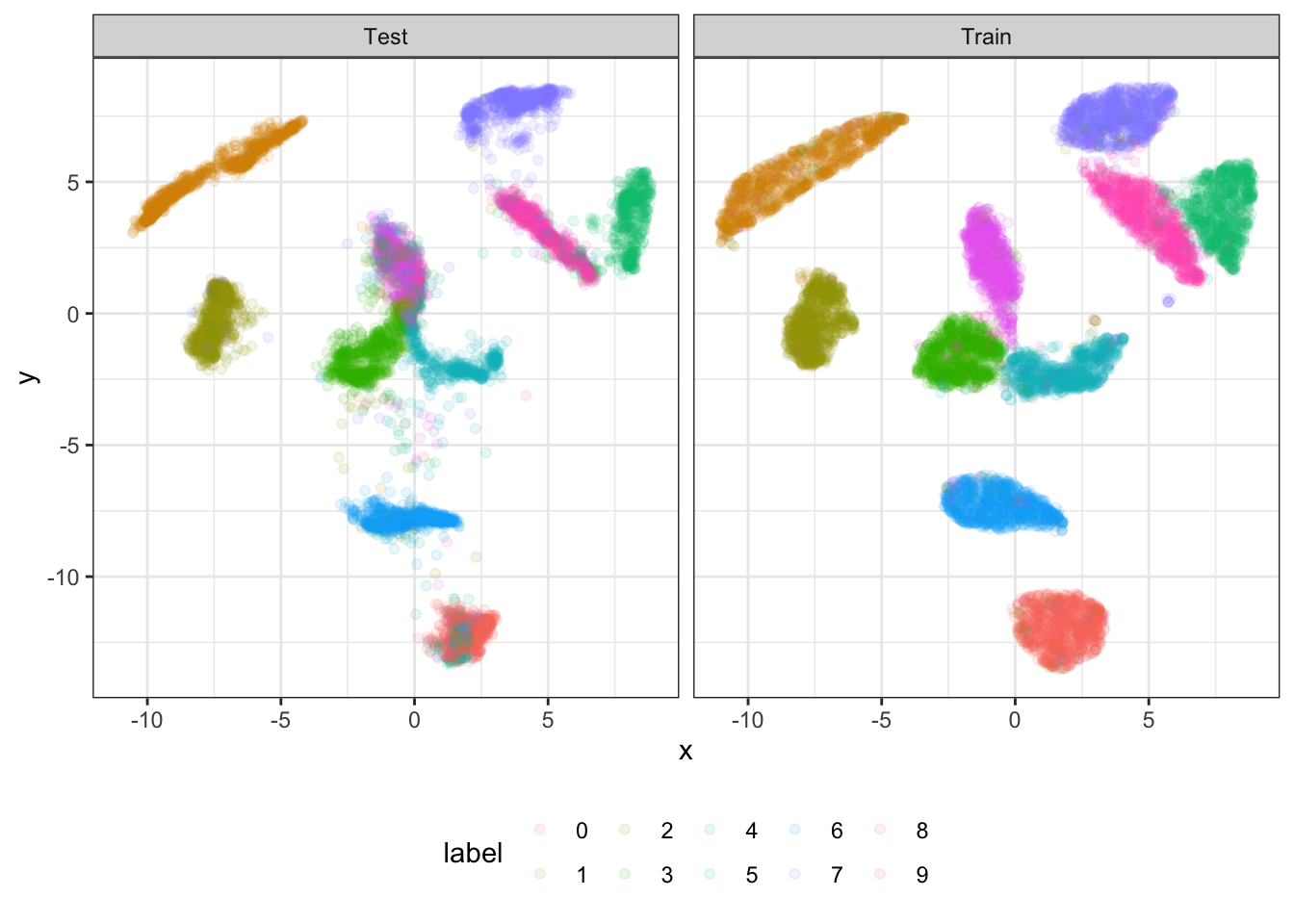
Figure 1: 10,000 samples from the MNIST train and test data, respectively, projected onto a UMAP embedding trained on the full MNIST train data set.
We see that even the MNIST test data would not be predicted perfectly by a k-nearest neighbor classifier: Not only are some samples projected onto the “cluster” of a different class, but the margins between clusters are quite small. This makes it easy for a sample to fall into the correct cluster but to then be classified based on a neighbor from a neighboring cluster.
We can now project the Fashion MNIST data onto the same embedding to evaluate how good our classification performance is when all we have are five samples from Fashion MNIST and the pretrained MNIST embedding. In the following, UMAP_1NN corresponds to the approach of embedding the data before classification via 1-nearest-neighbor, while RANDOM assigns a random label from the 10 classes and RANDOM_SHOT picks the label randomly from one of the \(n\) training examples.
| UMAP_1NN | RANDOM | RANDOM_SHOT |
|---|---|---|
| 0.369 | 0.101 | 0.199 |
When we consider the accuracy by class, we observe that some classes are easier to predict than others.
| CLASS | UMAP_1NN | RANDOM | RANDOM_SHOT |
|---|---|---|---|
| 0 | 0.436 | 0.106 | 0.204 |
| 1 | 0.426 | 0.109 | 0.188 |
| 2 | 0.325 | 0.089 | 0.189 |
| 3 | 0.341 | 0.105 | 0.197 |
| 4 | 0.435 | 0.108 | 0.206 |
| 5 | 0.297 | 0.103 | 0.198 |
| 6 | 0.233 | 0.091 | 0.198 |
| 7 | 0.434 | 0.093 | 0.208 |
| 8 | 0.349 | 0.103 | 0.210 |
| 9 | 0.413 | 0.104 | 0.193 |
To put these results into context, we perform a couple of other combinations: We can vary the training data for the UMAP embedding (use either the MNIST or the Fashion MNIST training set), and then evaluate how well we can predict the corresponding test sets. Here, it is especially interesting to compare how well we can predict MNIST using an MNIST embedding, and Fashion MNIST using a Fashion MNIST embedding–this is essentially the best we can hope for when predicting Fashion MNIST using MNIST embedding, and MNIST using the Fashion MNIST embedding.
Additionally, we can vary the number of few shot examples. Note that we always include exactly one sample from the correct class to have any chance of “learning” the new concept. This means, however, that with two samples we have a 50-50 chance of randomly assigning the correct class. Thus it’s important to compare the UMAP_1NN performance against the performance of picking a random sample from the few shots (column RS).
Looking at the results, there are a few things to note.
First, observe how the performance generally degredates as the number of few shot training examples increases: Apparently this increases the chances of picking the wrong neighbor, since the share of training examples with the correct class drops from 50% to 20% to 10%—this is also seen in the RS column. As we add more training examples, chances increase that an example from a wrong class is embedded close to the test observation. If we could increase the training observations much more as well as the number of examples from the correct class, the performance should improve with \(n\) as usually expected.
Note that we can predict Fashion MNIST better than random using the MNIST embedding; but we essentially predict randomly when classifying numbers given the Fashion MNIST embedding. This is somewhat surprising given that classifying Fashion MNIST is generally harder than classifying MNIST. Yet, the MNIST embedding appears more useful for the task at hand.
Also note that we can predict the test sets quite well if we use the embedding trained on the corresponding train set: We achieve a 60% accuracy for both Fashion MNIST and MNIST when using 10 training samples.4 Maybe we would actually expect better results given how simple MNIST is?
| UMAP | TRAIN | TEST | n | UMAP_1NN | R | RS |
|---|---|---|---|---|---|---|
| MNIST Train | F-MNIST Train | F-MNIST Test | 2 | 0.62 | 0.10 | 0.49 |
| MNIST Train | F-MNIST Train | F-MNIST Test | 5 | 0.37 | 0.09 | 0.20 |
| MNIST Train | F-MNIST Train | F-MNIST Test | 10 | 0.26 | 0.10 | 0.10 |
| MNIST Train | MNIST Test | MNIST Test | 2 | 0.84 | 0.10 | 0.50 |
| MNIST Train | MNIST Test | MNIST Test | 5 | 0.69 | 0.10 | 0.20 |
| MNIST Train | MNIST Test | MNIST Test | 10 | 0.60 | 0.10 | 0.10 |
| F-MNIST Train | MNIST Train | MNIST Test | 2 | 0.52 | 0.10 | 0.51 |
| F-MNIST Train | MNIST Train | MNIST Test | 5 | 0.22 | 0.10 | 0.20 |
| F-MNIST Train | MNIST Train | MNIST Test | 10 | 0.12 | 0.11 | 0.10 |
| F-MNIST Train | F-MNIST Test | F-MNIST Test | 2 | 0.90 | 0.10 | 0.50 |
| F-MNIST Train | F-MNIST Test | F-MNIST Test | 5 | 0.74 | 0.10 | 0.20 |
| F-MNIST Train | F-MNIST Test | F-MNIST Test | 10 | 0.60 | 0.10 | 0.10 |
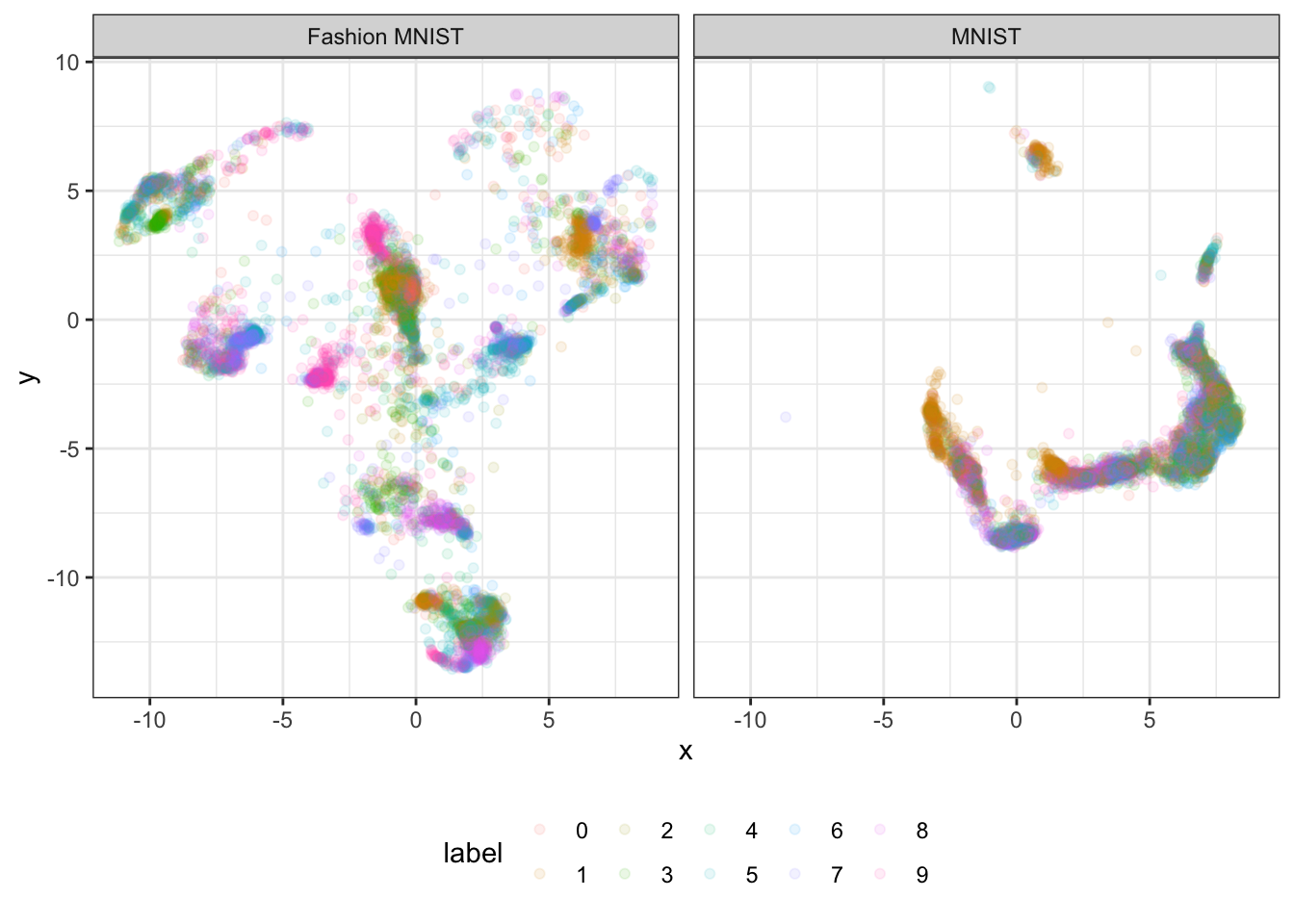
Figure 2: This figure shows the MNIST test set projected onto a UMAP embedding trained on the Fashion MNIST train data. Also, the Fashion MNIST test set projected onto a UMAP embedding trained on the MNIST train data. In contrast to figure 1 above, we see that the projection across data sets does not work too well.
Questions Raised by This Approach
Let me be clear that my quick’n’dirty experiment above does not follow the procedure of Tian et al. (2020) too closely: They use a CNN trained for classification as feature extractor (“embedding”) which probably makes more sense than UMAP to embed new “unseen” classes (it also returns more dimensions than just the two I have). Also, I use MNIST and Fashion MNIST which are not used for few-shot learning evaluation.
Still, I wonder: If I would be faced with an “actual” few-shot learning task in the real world, would I like to rely on some embedding? How do I know that the feature extractor will extract features from my few training samples in a useful way? I certainly wouldn’t have sufficient samples to evaluate the quality of the (pre-trained) embedding for my new images.
Indeed, the evaluation setup used in Tian et al. (2020) (and, most likely, in the remaining few-shot learning literature) feels too easy: The evaluation only checks whether an approach that has access to a large set of training samples from ImageNet (e.g., bike, panda, cat, …) can learn to classify new classes from ImageNet (e.g., car, chair, dog, …) from few samples. What surprises is me is how related the images are allowed to be—the test of generalization does not appear difficult enough. It’s not like we allow some pre-training on ImageNet and then try to classify different diseases based on CT scans.
The code used to produce these results is available on Github.
References
Thomas Cover, P.E. Hart (1967). Nearest Neighbor Pattern Classification. IEEE Transactions on Information Theory, Vol. IT-13, No. 1.
Yann LeCun, Corinna Cortes, Christopher J.C. Burges. The MNIST database of handwritten digits. http://yann.lecun.com/exdb/mnist/
Leland McInnes, John Healy, James Melville (2018). UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. https://arxiv.org/abs/1802.03426
Yonglong Tian, Yue Wang, Dilip Krishnan, Joshua B. Tenenbaum, Phillip Isola (2020). Rethinking Few-Shot Image Classification: a Good Embedding Is All You Need?. https://arxiv.org/abs/2003.11539
Han Xiao, Kashif Rasul, Roland Vollgraf (2017). Fashion-MNIST: a Novel Image Dataset for Benchmarking Machine Learning Algorithms. https://arxiv.org/abs/1708.07747
Though I cannot say that I’m familiar with the literature; so maybe these approaches are actually quite simple.↩
We did not use the label information as in metric learning though this would be a nice additional step to explore.↩
Here we ensure that exactly one of the five training samples has the same label as the test observation.↩
Note that we sample the training examples from the test set: In theory, we might sometimes have the same observation in both the few shot examples and the observation to be classified. Given the sample sizes the chance is small, but nonetheless it might have given a slight positive bias.↩